BLOQUE I: UTILIZA ANGULOS, TRIANGULOS Y RELACIONES METRICAS

 

* ANGULOS: 

Figura formada por dos semirrectas que parten del mismo punto inicial. A las dos rectas se les denomina lados del ángulo y al punto inicial se le llama vértice del ángulo. El símbolo del ángulo es ..

 -Por su overtura

 

Un ángulo se forma cuando dos líneas rectas se unen. La amplitud del giro de un ángulo se puede medir, y la unidad que se utiliza para expresarlo se llama grado. Si se realiza una vuelta completa, el ángulo mide 360 grados, escrito esto como 360°.		Media vuelta completa (lo que significa pasar justo al lado opuesto) es un giro de 180°. Este tipo de ángulo se llama ángulo llano.
Un cuarto de vuelta es un giro de 90°, también llamado ángulo recto.		Si un ángulo tiene menos de 90°, se llama ángulo agudo.
Si un ángulo tiene más de 90°, pero menos de 180°, se llama ángulo obtuso.		Si un ángulo mide más de 180°, se llama ángulo cóncavo.
Si un ángulo tiene menos de 180°, se llama ángulo convexo.		Si un ángulo tiene 0°, se llama ángulo nulo.

-Por la posicion entre dos rectas paralelas y una secante:

 

Observa en el dibujo que dos rectas paralelas cortadas una recta transversal crea 8 ángulos que reciben distintos nombres según la posición que ocupan:

Las recta r corta a las rectas paralelas m y n:

Los nombres de los ángulos según el lugar que ocupan reciben los nombres:

Interiores o internos:

En azul, son los que se encuentran entre las rectas paralelas.

Ángulos exteriores o externos:

Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.

Ángulos correspondientes:
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.

Los ángulos del mismo color son correspondientes:

El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’

Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.

Ángulos alternos internos

Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:

Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.

 Ángulos alternos externos:

Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:

Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.

15.55   Observa la figura siguiente y después, contesta a las preguntas siguientes:

1. ¿Cómo son los ángulos 1 y 2?
2. ¿Cómo podemos llamar a los ángulos 1 y 4?
3. ¿Son suplementarios los ángulos 2 y 4?
4. ¿Son iguales los ángulos 2 y 3? ¿Por qué?
5. ¿Son correspondientes los ángulos 3 y 7?
6. ¿Cómo son los ángulos 4 y 6?
7. ¿Es el ángulo 6  correspondiente al ángulo 3?
8. ¿Son iguales los ángulos 5 y 8? ¿Por qué?
9. ¿Cómo puedes llamarles a los ángulos 1 y 8?
10. ¿Son alternos internos los ángulos 5 y 6?

Respuestas:

1. Adyacentes y suplementarios.
2. Opuestos por el vértice. Uno es externo y el otro interno.
3. Sí, juntos valen 180º.
4. Sí, por ser opuestos por el vértice.
5. Sí por encontrarse en el mismo lado de la secante, siendo uno un ángulo interior y el otro un ángulo exterior.
6. No porque aunque se encuentren en el mismo lado de la secante los dos son ángulos interiores.
7. No porque no están situados al mismo lado de la secante y además, los dos son interiores.
8. Sí por estar opuestos por el vértice.
9. Son ángulos alternos externos ya que se encuentran a distinto lado de la secante y en la parte exterior de las paralelas.
10. No porque no son alternos y además, los alternos internos son iguales entre sí. 

-Por las suma de sus medidas:

 

	Ángulos complementarios: dos ángulos son complementarios si suman 90°
	Ángulos suplementarios: dos ángulos son suplementarios si suman 180°.

-Complementarios:

 Dos ángulos son complementarios si la suma de sus grados es igual a 90º.^o.

Si conocemos un ángulo, su ángulo complementario se puede averiguar restando la medida del mismo a 90^o.

Se llama al complemento de un ángulo a lo que le falta a éste para valer un ángulo recto.

Ejemplo:

 ¿Cuál es el ángulo complementario de 43^o?
Solución: 90^o  -  43^o  =  47^o
 ¿Cuál es el ángulo complementario de 62º?
90º - 62º = 28º

¿Cuál es el ángulo complementario de 43º?
90º - 43º = 47º
 

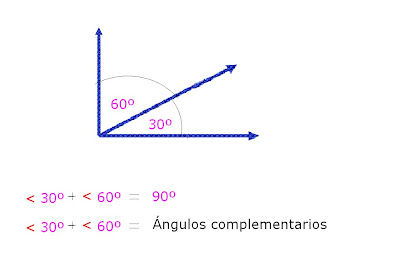
-Suplementarios :

Dos ángulos son suplementarios si la suma de sus grados es igual a 180^o.
Si conocemos un ángulo, su ángulo suplementario se puede averiguar restando la medida del mismo a 180^o.

Los ángulos suplementarios son los que sumados valen dos ángulos rectos, o sea, 180º.

Ejemplo:

¿Cuál es el ángulo suplementario de 143^o?
Solución: 180^o  -  143^o  =  37^o

 

*TRIANGULOS :

El triángulo está determinado por tres segmentos de recta que se denominan lados, o por tres puntos no alineados llamados vértices.

Los lados de un triángulo se escriben en minúscula, con las mismas letras de los vértices opuestos.

Los vértices de un triángulo se escriben con letras mayúsculas.

Los ángulos de un triángulo se escriben igual que los vértices.


-POR LA MEDIDA DE SUS LADOS:

Triángulo equilátero

Tres lados iguales.

Triángulo isósceles

Dos lados iguales.

Triángulo escaleno

Tres lados desiguales.

 

 

-POR LA OVERTURA DE SUS ANGULOS:

 

Triángulo acutángulo

Tres ángulos agudos

Triángulo rectángulo

Un ángulo recto
El lado mayor es la hipotenusa.
Los lados menores son los catetos.

Triángulo obtusángulo

Un ángulo obtuso.

*PROPIEDADES RELATIVAS DE LOS TRIANGULOS :

1 Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.

a < b + c

a > b - c

2La suma de los ángulos interiores de un triángulo es igual a 180°.

A + B + C =180º

3 El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes.

α = A + B

α = 180º - C

5 Si un triángulo tiene dos lados iguales, sus ángulos opuestos también son iguales.

BLOQUE II: COMPRENDE LAS CONGRUENCIAS DE LOS TRIANGULOS.

*CRITERIOS DE CONGRUENCIA:

Los criterios de congruencia de triangulos  nos dicen que no es necesario verificar la congruencia de los 6 pares de elementos ( 3 pares de lados y 3 pares de ángulos), bajo ciertas condiciones, podemos verificar la congruencia de tres pares de elementos.

-L,L,L  :

 

 Dos triángulos son congruentes si sus tres lados son respectivamente iguales.
a ≡ a’
b ≡ b’
c ≡ c’
→ triáng ABC ≡ triáng A’B'C’

-L,A,L:

 Dos triángulos son congruentes si son respectivamente iguales dos de sus lados y el ángulo comprendido entre ellos.
b ≡ b’
c ≡ c’
α ≡ α’
→ triáng ABC ≡ triáng A’B'C’

 -A, L, A:

Dos triángulos son congruentes si tienen un lado congruente y los ángulos con vértice en los extremos de dicho lado también congruentes. A estos ángulos se los llama adyacentes al lado.
b ≡ b’
α ≡ α’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’

 Ejercicios:

 

Ejercicio Nº01

En la figura triangulo ABC-triangulo BDF, además AB=AC; AB=3cm; CB=4cm y FD=BC/2. ¿cuánto mide el perímetro de la figura?
A) 10       B) 12            C) 13           D) 15            E) 18

Ejercicio Nº02

Triangulo ABC es rectángulo en A,FD es simetral de BC; BC=10 y AC=6, entonces la medida de FD es:
A) 3,75            B) 3              C) 9,6               D) 6,25              E) 4

Ejercicio Nº03

Si en la figura se tiene que BC//DE, entonces ¿Cuál de las afirmaciones es (son) verdadera (s)?
I) AB/BC = AE/ED
II) BC/DE = AC/AE
III) AB/BC = BD/DE
A) Solo I              B) Solo II            C) Solo III            D) Solo I y II           E) Solo I y III

Ejercicio Nº04

Se puede afirmar que el triangulo ABC es semejante con el triangulo PQR si:
1) AB/PQ=BC/QR=CA/RP
A) (1) por si sola             B) (2) por si sola          C) Ambas juntas, (1) y (2)
D) Cada una por si sola (1) ó (2)                         E) Se requiere información adicional.

Ejercicio Nº05

Los lados de un poligono miden 6,9,12 y 15cm respectivamente, ¿cual es el perímetro de otro polígono semejante al anterior si su lado mayor mide 20cm?
A) 31,5              B) 36            C) 40            D) 50,5                E) 56

Ejercicio Nº06

En la figura, DC perpendicular AB, Si AD=DB, entonces el triangulo DAC es congruente con el triangulo:
A) BCD               B) DCB           C) DBC              D) CBD                  E) BDC

Ejercicio Nº07

Si los lados de 2 triángulos estan en la razón 2:5, entonces sus áreas están en la razón:
A) 25:2          B) 4:25             C) 5:4          D) 2:5             E) No se puede determinar

Ejercicio Nº08

En el triangulo ABC de la figura se traza una recta L que corta a los lados AC y BC en M y N de modo que el triangulo que se forma (triangulo MNC) es semejante al triangulo BAC: Si la recta L no es paralela al lado AB. ¿Cuál (es) delas afirmaciones siguientes es (son) verdadera (s)?
I) MN:AB = CN:AC
II) CM:CA = CN:CB
III) MN:CM = AB:AC
A) Solo I              B) Solo II             C) Solo III           D) Solo II y III             E) I, II y III

 BLOQUE III: RESUELVE PROBLEMAS DE SEMEJANZA DE TRIANGULOS Y TEOREMA DE PITAGORAS

*CRITERIOS DE SEMEJANZA:

1Dos triángulos son semejantes si tienen dos ángulos iguales.

2 Dos triángulos son semejantes si tienen los lados proporcionales.

3 Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.

Ejercicios

Razona si son semejantes los siguientes triángulos:

Son semejantes porque tienen los lados proporcionales.

180º − 100º − 60º = 20º

Son semejantes porque tienen dos ángulos iguales.

Son semejantes porque tienen dos lados proporcionales y un ángulo igual.

*TEOREMA DE TALE:

Cuando en geometría hablemos del Teorema de Tales (o Thales), debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.
El primero de ellos se refiere a la construcción de un triángulo que sea semejante a otro existente (triángulos semejantes son los que tienen iguales ángulos).
Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (los circuncentros se encuentran en el punto medio de su hipotenusa).

Primer teorema

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
Entonces, veamos el primer Teorema de Tales en un triángulo:

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC. Lo que se traduce en la fórmula

Ejercicios

1.Las rectas a, b y c son paralelas. Halla la longitud de x.

2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí, porque se cumple el teorema de Thales.

El teorema de Thales en un triángulo

Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.

Hallar las medidas de los segmentos a y b.

Aplicaciones del teorema de Thales

El teorema de Thales se utiliza para dividir un segmento en varias partes iguales.

Ejemplo

Dividir el segmento AB en 3 partes iguales

1. Se dibuja una semirrecta de origen el extremo A del segmento.

2. Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A.

3. Por cada una de las divisiones de la semirrecta se trazan rectas paralelas al segmento que une B con la última división sobre la semirrecta. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.

*TEOREMA DE PITAGORAS

En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Conclusión: Del teorema anterior deducimos lo siguiente:

1. En todo triángulo rectángulo, la hipotenusa es igual a la raíz cuadrada de la suma de los cuadrados de los catetos.
   
   
   

2. En todo triángulo rectángulo, cada cateto es igual a la raíz cuadrada de la hipotenusa al cuadrado, menos el cuadrado del otro cateto.
   
   
   
   

Aplicaciones del teorema de Pitágoras

EJERCICIOS

1La hipotenusa de un triángulo rectángulo mide 30 cm y la proyección de un cateto sobre ella 10.8 cm. Hallar el otro cateto.

2En un triángulo rectángulo, las proyecciones de los catetos sobre la hipotenusa miden 4 y 9 metros. Calcular la altura relativa a la hipotenusa.

3La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:

1 Los catetos.

2 La altura relativa a la hipotenusa.

3 El área del triángulo.

4Calcular los lados de un triángulo rectángulo sabiendo que la proyección de uno de los catetos sobre la hipotenusa es 6 cm y la altura relativa de la misma cm.

5Una escalera de 10 m de longitud está apoyada sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la pared?

6Determinar el lado de un triángulo equilátero cuyo perímetro es igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus áreas?

7Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio 6 cm.

8 Determinar el área del cuadrado inscrito en una circunferencia de longitud 18.84 m.

9 En un cuadrado de 2 m de lado se inscribe un círculo y en este círculo un cuadrado y en este otro círculo. Hallar el área comprendida entre el último cuadrado y el último círculo.

10 El perímetro de un trapecio isósceles es de 110 m, las bases miden 40 y 30 m respectivamente. Calcular los lados no paralelos y el área.

11 Si los lados no paralelos de un trapecio isósceles se prolongan, quedaría formado un triángulo equilátero de 6 cm de lado. Sabiendo que el trapecio tiene la mitad de la altura del triángulo, calcular el área del trapecio.

12 El área de un cuadrado es 2304 cm². Calcular el área del hexágono regular que tiene su mismo perímetro.

13En una circunferencia de radio igual a 4 m se inscribe un cuadrado y sobre los lados de este y hacia el exterior se construyen triángulos equiláteros. Hallar el área de la estrella así formada.

14 A un hexágono regular 4 cm de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada.

15 En una circunferencia una cuerda de 48 cm y dista 7 cm del centro. Calcular el área del círculo.

16 Los catetos de un triángulo inscrito en una circunferencia miden 22.2 cm y 29.6 cm respectivamente. Calcular la longitud de la circunferencia y el área del círculo.

17Calcular el área de la corona circular determinada por las circunferencias inscrita y circunscrita a un cuadrado de 8 m de diagonal.

18Sobre un círculo de 4 cm de radio se traza un ángulo central de 60°. Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente.

19 Dado un triángulo equilátero de 6 m de lado, hallar el área de uno de los sectores determinado por la circunferencia circunscrita y por los radios que pasan por los vértices.

20Calcular el área de la corona circular determinada por las circunferencias inscrita y circunscrita a un cuadrado de 8 m de diagonal.

BLOQUE IV: RECONOCE LAS PROPIEDADS DE LOS POLIGONOS

*POLOGONOS: 

  Etimológicamente, la palabra “POLÍGONO” proviene de las raíces “POLI” que significa “muchos” y “GONOS” que significa “ángulos”; por lo tanto, es un trazo que contiene muchos ángulos.

Los polígonos se nombran mediante letras mayúsculas situadas en lo vértices del mismo, después de la palabra “Polígono”.

En un polígono hay que considerar:

• LADOS: Son las rectas que limitan al polígono.
• ÁNGULOS INTERNOS: Son los formados por los lados consecutivos.
• ÁNGULOS EXTERNOS: Son los formados por un lado y la prolongación de lado adyacente.
• VÉRTICES: Son los extremos comunes de cada dos segmentos consecutivos.
• DIAGONALES: Son las rectas que unen dos vértices no consecutivos del polígono.
  
  

POLIGONAL ABIERTA: Son los segmentos que no pertenece a una misma recta.

POLIGONAL CERRADA: Es una poligonal en la que el extremo del último segmento y el origen del primero coinciden.

CLASIFICACIÓN DE LOS POLÍGONOS

1. Según el carácter entrante o saliente de los ángulos del polígono se distingue lo siguiente:
   
   a) POLÍGONOS CONVEXOS: Cuando tienen todos sus lados salientes, es decir, tienen todos sus ángulos menores que 180°.
   
   

b) POLÍGONOS CONCAVOS: Cuando tienen algún ángulo entrante, es decir, uno ó más de sus ángulos interiores son mayores de 180°.

2. Según la regularidad de sus elementos se distingue lo siguiente:
   
   a) POLÍGONOS REGULARES: Son aquellos que tienen sus lados y ángulos iguales.
   
   

b) POLÍGONO IRREGULAR: Son aquellos que no tienen todos sus lados y ángulos iguales.

·  Según el número de lados, algunos polígonos reciben nombres específicos.

 

 *ELEMENTOS Y PROPIEDADES:

Vértice (V): Punto donde concurren dos lados.

Lados (L): Segmentos que limitan al polígono.

Centro (C): Punto interior que equidista de cada vértice.

Radio (r): Segmento que une el centro con un vértice.

Apotema (a): Segmento que une el centro con el punto medio de un lado y es perpendicular al mismo.

Ángulo central (α): Es el ángulo formado por dos radios consecutivos.

                              Se calcula     Ángulo central = 360° : n       ,                                                                                                                                     donde n es el número de lados del polígono.     

Ángulo interior (β): Es el águlo formado por dos lados consecutivos
                         
                 Para calcular la suma de
                 todos los ángulos interioresSAI 180 . (n - 2)
         Para calcular un ángulo interior

Ángulo interior = SAI : n

Ángulo exterior (γ): Es el ángulo formado por un lado y la prolongación de otro lado
consecutivo al primero.

               Suma de ángulos exteriores = 360°
              Un ángulo exterior

 360° : n


     ¿Cómo se calcula el área de un polígono regular?

      Si observas bien la figura, verás que puedes hallar el área del polígono sumando
        las áreas de los triángulos iguales.            

*ANGULO CENTRAL:

Es el formado por dos radios consecutivos.

Si n es el número de lados de un polígono:

Ángulo central = 360° : n

Ángulo central del pentágono regular= 360° : 5 = 72º

*ANGULO INTERIOR:

Es el formado por dos lados consecutivos.

Ángulo interior =180° − Ángulo central

Ángulo interior del pentágono regular = 180° − 72º = 108º

EJERCICIOS:

¿Cuánto mide los ángulos interiores de un polígono de 20 lados?
A) 3200º              B) 3240º                C) 3160º                D) 3300º               E) 3500º

En al figura el triángulo AED es equilátero y EBCD es un rombo. Si CF perpendicular AB y DC=4, entonces ¿cuál es el área de la región sombreada?
A) 2√3           B) 4√3              C) 6√3             D) 5√3          E) 12√3

El hexágono de la figura tiene lado √12, entonces ¿cuál es el área del trapecio ABCD?
A) 18√3         B) 9√3            C) 6√3            D) 24√3             E) 12√3

En el pentágono regular de la figura, ¿Cuál es el valor de x?
A) 540         B) 108           C) 72         D) 38           E) 36

Determinar el área de un trapecio si su altura es 5cm.
(1) Su mediana es 7cm
(2) La diferencia de sus bases es 4cm.
A) (1) por si sola                 B) (2) por si sola             C) Ambas juntas, (1) y (2)
D) Cada una por si sola (1) ó (2)                                E) Se requiere información adicional

Link de tutorías:  http://profe-alexz.blogspot.mx/2012/02/poligonos-angulos-y-areas-psu.html

*LA SUMA DE LOS ANGULOS CENTRALES, INTERIORES Y EXTERIORES:

Si n es el número de lados de un polígono:

S = (n − 2) · 180°.

Suma de ángulos de un triángulo = (3 − 2) · 180° = 180º.

Suma de ángulos de un cuadrilátero = (4 − 2) · 180° = 360º.

Suma de ángulos de un pentágono = (5 − 2) · 180° = 540º.

Suma de ángulos de un hexágono = (5 − 2) · 180° = 720º.

*PERIMETRO Y AREA DE LOS POLIGONOS:

Nombre	Dibujo	Perímetro	Área
Triángulo		P = Suma de los lados P = b + c + d	p = semiperímero
Cuadrado		P = 4 · a	A = a2
Rectángulo		P = 2(b + a)	A = b · a
Rombo		P = 4 · a
Romboide		P = 2(b + c)	A = b · a
Trapecio		P = B + c + b + d
Trapezoide		P = a + b + c + d	A = Suma de las áreas de los dos triángulos
Polígono regular

link de tutorías : http://profe-alexz.blogspot.mx/2011/04/areas-y-perimetros-38-ejercicios.html

 BLOQUE V: EMPLEA LA CIRCUNFERENCIA

*CIRCUNFERENCIA:

La circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.

Elementos de la circunferencia

Centro de la circunferencia

El centro es el punto del que equidistan todos los puntos de la circunferencia.

Radio de la circunferencia

El radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.

Cuerda

La cuerda es un segmento que une dos puntos de la circunferencia.

Diámetro

El diámetro es una cuerda que pasa por el centro de la circunferencia.

El diámetro mide el doble del radio.

Arco

Un arco es cada una de las partes en que una cuerda divide a la circunferencia.

Se suele asociar a cada cuerda el menor arco que delimita.

Semicircunferencia

Una semicircunferencia es cada uno de los arcos iguales que abarca un diámetro.

Longitud de una circunferencia

La longitud de una circunferencia es igual a pi por el diámetro.

La longitud de una circunferencia es igual a 2 pi por el radio.

Ejercicios de la longitud de una circunferencia.

Ángulos en la circunferencia

Ángulo central

El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.

La medida de un arco es la de su ángulo central correspondiente.

Ángulo inscrito

El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.

Mide la mitad del arco que abarca.

Ángulo semiinscrito

El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.

Mide la mitad del arco que abarca.

Ángulo interior

Su vértice es interior a la circunferencia y sus lados secantes a ella.

Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

Ángulo exterior

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:

Mide la mitad de la diferencia entre las medidas de los arcos que abarcan sus lados sobre la circunferencia.

Posiciones relativas de un punto respecto a una circunferencia

Interior

La distancia del punto al centro es menor que el radio.

Punto sobre la circunferencia.

El punto pertenece a la circunferencia.

Punto exterior a la circunferencia

La distancia del punto al centro es mayor que el radio.

Posiciones relativas de una recta y una circunferencia

Recta secante

La recta corta a la circunferencia en dos puntos.

Recta tangente

La recta corta a la circunferencia en un punto.

Recta exterior

No tiene ningún punto de corte con la circunferencia.

Posiciones relativas de dos circunferencias

Ningún punto en común

Exteriores

La distancia entre los centros es mayor que la suma de las radios.

Interiores

La distancia entre los centros es menor que la diferencia de los radios.

Concéntricas

Los centros coinciden.

Un punto común

Tangentes exteriores

La distancia entre los centros es igual a la suma de los radios.

Tangentes interiores

La distancia entre los centros es igual a la diferencia de los radios.

Dos puntos en común

Secantes

La distancia entre los centros es mayor que la diferencia de los radios.

-RECTAS Y SEGMENTOS:


 Desde el punto de vista geométrico, el estudio del círculo ha resultado ser muy interesante, y lo es más cuando se logra encontrar la relación que existe entre los elementos que lo constituyen.

Hay una gran cantidad de cuerpos y objetos que presentan esta figura, como el caso de una moneda, la base de recipientes en forma cilíndrica, la rueda de una bicicleta, etcétera.

Antes de profundizar en el tema, es conveniente considerar que no hay que confundir lo que es la circunferencia con el círculo; por ello se procede a identificar ambas partes en la siguiente figura.





Como puede observarse en la figura anterior, el contorno es la circunferencia, en tanto que el interior es el círculo.

A continuación se identificaron las rectas que cortan o tocan a la circunferencia, así como la que se encuentra ubicada fuera de la misma.




La recta (1) corta la circunferencia en dos puntos; por lo tanto, se tiene que los puntos de esta recta son tanto interiores como exteriores a la circunferencia. Este tipo de rectas son conocidas como secantes.

La recta (2) toca a la circunferencia en un solo punto, el cual recibe el nombre de punto de tangencia; los demás puntos de la recta se localizan en el exterior de la circunferencia. Este tipo de rectas son conocidas como tangentes.

La recta (3) se encuentra fuera de la circunferencia, es decir, se ubica en el exterior de la misma y, por no tener ningún punto de contaco con ella, se le conoce como recta exterior.

Ahora se identificaron, en la siguiente figura, los segmentos y arcos que se pueden trazar en el círculo o en la circunferencia, según sea el caso.



Como puede observarse, en la figura se han trazado los siguientes segmentos de recta.

El segmento AB es un radio del círculo. Cada punto de la circunferencia es el extremo de otro radio. Un radio es el segmento que une al centro del círculo con un punto cualquiera de la circunferencia.

El segmento CD es una cuerda del círculo. Cada par de puntos de la circunferencia determina una cuerda del circulo una cuerda es un segmento que une dos puntos cualesquiera de la circunferencia.

El segmento GH es un diámetro del círculo. El diametro del círculo es un segmento que une dos puntos de la circunferencia y pasa por el centro del círculo; se le considera como la cuerda de mayor tamaño que divide al círculo en dos partes congruentes

LM es un arco del círculo. Se define un arco como la parte continua de la circunferencia, limitada o comprendida entre dos puntos extremos, y se escribe para representarlo.

-ANGULOS:

Ángulo central es el ángulo que tiene su vértice en el centro de la circunferencia y los lados son radios de ella.		La medida del arco AB es la del ángulo central AOB. Arco AB = Angulo AOB
Arco AB = Ángulo AOB Esta igualdad nos permite medir en función del ángulo central o arco el resto de ángulos que pueden definirse en la circunferencia.
Angulo inscrito es aquel que tiene su vértice en  la circunferencia.El ángulo semiinscrito, (uno de los segmentos secante y el otro tangente) es un caso particular, o caso límite.		El ángulo inscrito mide la mitad que el arco que comprende.
Angulo interior, tiene su centro en un punto interior del círculo.		La medida del ángulo interior es la semisuma de los arcos que comprenden él y su opuesto.
Ángulo exterior es aquel que tiene su vértice en un punto exterior de la circunferencia, pudiendo ser sus lados, tangentes o secantes a la misma.		La medida del ángulo exterior es la semidiferencia de los arcos que abarca.

 -PERIMETRO Y AREA:

Longitud de una circunferencia

Ejemplo

1º Calcular la longitud de una rueda de 90 cm de diámetro.

1º A partir del diámetro

2º A partir del radio

 


 AREA
Medida de la superficie limitada por la circunferencia.
Su fórmula es A = π * r²
Donde π es la constante de valor 3.14592….. (que podemos redondear a 3.1416) Y r es la medida del radio del círculo

Ejemplo 1
Si se tiene una círculo de 10 cm de radio ¿cuál será su área?
A = 3.1416 * (10 cm)²
A = 3.1416 * 100 cm²
A = 314.16 cm²
Ejemplo 2
Si un círculo tiene 900 cm2 de área. ¿Cuánto mide su radio?
Despejando r de la fórmula original se tiene
r² = A/π
De donde se deduce que r = √(A/π)
Para nuestro ejemplo r =√(900 cm²/3.1416)
r = 16.93 cm

Deducción área del círculo mediante el uso de la geometría

¿Cómo se llama la line que pasa por el centro y divide
al la circunferencia en dos parte iguales?

selecciona la opcion que conteste correctamente
la  pregunta.

radio

círculo

perímetro

 diámetro

¿Cómo se llama la line que va del centro de la
 circunferencia hasta cualquier extremo de la misma ?

selecciona la opcion que conteste correctamente
la  pregunta.

diámetro

 radio

área

perímetro

¿Cómo se llama el número especial que los Griegos?
descubrieron como la relacion que existe entre la
circunferencia y el diámetro?

 pi

17

316

número primo

selecciona la opcion que conteste correctamente
la  pregunta.

¿Cuál es el valor de pi?

selecciona la opcion que conteste correctamente
la  pregunta.

13.1416

 3.1416

3.1614

ninguno de los tres

 el símbolo

el símbolo

el símbolo

el símbolo

¿Cuál de estos símbolos hace referencia a pi ?

selecciona la opcion que conteste correctamente
la  pregunta.

∑

€

£

π

37.6992 cm

73.1245 cm

21.3256 cm

37.6299 cm

Escoje la opción que tenga correctamente
el perímetro de la circunferencia

12cm

52.3257 cm

50.2656 cm

50.2566 cm

50.6562 cm

Escoje la opción que tenga correctamente
el perímetro de la circunferencia

16cm

21.1299  cm

21.9912  cm

21.9212

21.3256  cm

Escoje la opción que tenga correctamente
el perímetro de la circunferencia

 cm

7 cm

b  x  a

l  x  l

   π  x diámetro

 ^{b  x  a}

selecciona la opcion que conteste correctamente
la  pregunta.

¿Cuál es la formula que determina el perímetro de
la circunferencia

2

si una circunferencia  mide de perímetro 28.2744 cm
¿cuanto mide su diámetro?

 9 cm

10 cm

8 cm

12 cm

BLOQUE VI :DESCRUBE LAS RELACIONES TRIGONOMETRICAS PARA RESOLVER TRIANGULOS RECTANGULOS



*FUNCIONES TRIGONOMETRICAS:

Cada par de lados homólogos (que se ubican en la misma posición) de un triángulo rectángulo cuyos ángulos sean iguales serán proporcionales.

 Para que sea más fácil interpretar lo que se está explicando el típico triángulo de catetos de 3 cm y 4 cm, que tendrá su hipotenusa de 5 cm (Pitágoras). Dibujemos otros dos triángulos donde los catetos y la hipotenusa sean el doble y el triple (según corresponda.

La proporcionalidad también puede escribirse respecto a los lados homólogos.

         Lo importante a destacar es que el ángulo en todos los casos es el mismo.

Este hecho es importante ya que permite relacionar a los ángulos con la razón de la proporción de los lados. Esta relación presenta la propiedad de unicidad y la propiedad de completitud (para cada par de lados homólogos existe siempre un único valor (razón) relacionado con una determinada [existe y es única] amplitud angular), por lo tanto se establece una función, a las que llamaremos trigonométrica.

Funciones Trigonométricas:

Si dividimos:		llamaremos a esta función:
		Seno y la denotaremos por Sen(a)
		Coseno y la denotaremos por Cos(a)
		Tangente y la denotaremos por Tan(a)
		Cotangente y la denotaremos por Cot(a)
		Secante y la denotaremos por Sec(a)
		Cosecante y la denotaremos por Csc(a)

NOTA: Las funciones Seno y Cosecante son inversas. También son inversas las funciones Coseno y Secante. Finalmente son inversas las funciones Tangente con Cotangente.

Esto es:

Las funciones trigonométricas son funciones periódicas, repiten el valor de imagen cada 360º. De esa manera tenemos que:  cos 60º = cos 420º = 0,5

Grafiquemos, mediante tablas, las siguientes funciones tomando valores angulares desde 0º hasta 360º. Para facilitar el trabajo tomemos ángulos a intervalos de 45º:

Función Seno:

a	sen a
0	0
45	0,71
90	1
135	0,71
180	0
225	- 0,71
270	-1
315	- 0,71
360	0

Función Coseno:

a	cos a
0	1
45	0,71
90	0
135	-0,71
180	-1
225	0,71
270	0
315	0,71
360	1

Función Tangente:

a	tg a
0	0
45	1
90	////
135	- 1
180	0
225	1
270	////
315	- 1
360	0

//// significa que no se puede calcular el valor de la función, el resultado no existe (asíntota).

Función Cotangente:

a	Cotg a
0	////
45	- 1
90	0
135	1
180	////
225	- 1
270	0
315	////
360	- 1

Función Secante

a	sec a
0	1
45	1,41
90	////
135	-1,41
180	-1
225	1,41
270	////
315	1,41
360	1

Función Cosecante:

a	Cosec a
0	////
45	1,41
90	1
135	1,41
180	////
225	- 1,41
270	-1
315	- 1,41
360	////

ejercicios :

   1. Primero encontraremos el valor de la  ecuación que nos hace falta, en éste caso,    
              
        ya que sabemos que la función de  Coseno relaciona Lado Adyacente sobre 
             
        Hipotenusa, ya conocemos dichos  valores, nos faltaría encontrar Lado   
             
        Opuesto:

    2. Ahora conociendo el  valor que nos hacía falta (b), empezaremos a encontrar
        
        cada una de las funciones que hacen  falta:

  3.  Teniendo todas la Funciones procedemos a graficar:

   1. Resolvamos primero la Fracción Mixta

      Multiplicamos 2 x 3 y el resultado  lo sumamos con el 1 dándonos como  resultado 7/2.
             
  2. Ahora encontramos el valor que hace falta:

  Sustituimos valores:

   3.  Ahora conociendo b, encontramos las funciones correspondientes:

4. Seguidamente graficamos:

*SISTEMA SEXAGESIMAL Y CIRCULAR:

Sistema sexagesimal

El Sistema Sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de los ángulos.

1 h 60 min 60 s

1º 60' 60''

Suma

1 Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos; y se suman.

Ejemplo:

2 Si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirá a los minutos.

Ejemplo:

3 Se hace lo mismo para los minutos.

Ejemplo:

 

 

 Ejercicios:

  Expresar en complejo

7 950 segundos

 

Expresar en incomplejo de segundos.

2 h 48min 30 s

 

  

Realiza la siguiente suma:

6 h 13 min 45 s + 7 h 12 min 43 s + 6 h 33 min 50 s

Realiza el producto:

(128° 42' 36'') × 3

Halla el ángulo complementario y el suplementario de 25° 38' 40''

 

 .sistema circular

En este sistema la unidad de medida es el radián (rad).
Un radián es la medida del ángulo con vértice en el centro de la circunferencia y cuyos lados determinan sobre ella un arco de longitud igual al radio r. Se simboliza 1 rad.
                 

 

Un ángulo completo mide 2 rad (o simplemente 2).
Un ángulo llano mide  rad (o simplemente ).
Un ángulo recto mide rad (o simplemente   )..


*RAZONES TRIGONOMETRICAS DIRECTAS Y RECIPROCAS DE ANGULOS AGUDOS :

Las razones trigonométricas inversas se definen de la siguiente manera:

• La cosecante (abreviado como csc o cosec), razón recíproca del seno:

• La secante (abreviado como sec), razón recíproca del coseno:

• La cotangente (abreviado como cot), razón recíproca de la tangente:

Sea el ángulo BACde medida α (siempre menor de 90º) en el triángulo rectángulo ABC. Los lados BC y BA son los catetos y AC, la hipotenusa.

En este triángulo rectángulo, las razones trigonométricas con respecto a alfa (α) se definen como:

Seno

Seno, es la razón (división) entre el cateto opuesto al ángulo y la hipotenusa
Ver: PSU: Geometría;
Pregunta 09_2006
Pregunta 11_2006

Coseno

coseno, es la razón (división) entre el cateto adyacente al ángulo y la hipotenusa

Tangente

tangente, es la razón entre el cateto opuesto al ángulo y el cateto adyacente al mismo.
Estas tres (seno, coseno, tangente) son las razones fundamentales que se pueden establecer entre un ángulo agudo y los lados del triángulo rectángulo del cual forman parte.
A cada razón fundamental corresponde una razón recíproca, llamadas así por que cada una es la inversa de otra fundamental.
Las tres siguientes son las razones recíprocas que se pueden establecer respecto al mismo ángulo:

Cosecante

cosecante, es la razón entre la hipotenusa y el cateto opuesto al ángulo, y como es la recíproca del seno de α se puede expresar como

Secante

secante, es la razón entre la hipotenusa y el cateto adyacente al ángulo, y como es la reciproca del coseno de α se puede expresar como

Cotangente

cotangente, es la razón entre el cateto adyacente al ángulo y el cateto puesto al mismo, y como es la recíproca de la tangente de α se puede expresar como


Ahora, hagamos un ejercicio:
dado el triángulo ABC rectángulo en B (figura a la derecha).
Sean sus catetos AB = 8 cm y BC = 6 cm.
Aplicamos el Teorema de Pitágoras y calculamos la hipotenusa, que es:
8² + 6² = 10²; o sea, es igual a 10 cm
entonces podemos calcular las razones trigonométricas: